Entropy

Entropy : 불확실성 (uncertainty) 에 대한 척도 / 정보를 표현하는데 필요한 최소 평균 자원량

Entropy의 정의를 자세히 알아보자
아래에 상대방이 뽑은 카드를 맞추는 게임이 있다.

여기서 가장 간단하게 생각해서 맞출수 있는 방식은
1. a인지 물어본다. => < Yes> 일 경우 a
2. 1번이 < No>일 경우 b인지 물어본다. => < Yes> 일 경우 b
3. c인지 물어본다. => < Yes> 일 경우 c or < No> 일 경우 d

간단히 생각한 방식의 기댓값을 구해보면

카드 $(s_i)$	a	b	c	d
정답 카드를 뽑을확률 $(p_i = P(s_i))$	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$
이때 필요한 질문횟수 $(x_i)$	1	2	3	3

$E[X] = \sum_{i=1}^4p_ix_i = \frac{1}{4}\times1+\frac{1}{4}\times2+\frac{1}{4}\times3+\frac{1}{4}\times3 = 2.25$
평균 자원량이 2.25회 정도 된다.




다른방식을 사용해보자
1. {a, b}중에 있는지 물어본다. <Yes, No>
2. {a, b}중 있다면 a인지 물어본다. < No> 라면 c인지 물어본다.

카드 $(s_i)$	a	b	c	d
정답 카드를 뽑을확률 $(p_i = P(s_i))$	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$
이때 필요한 질문횟수 $(x_i)$	2	2	2	2

다른방식의 기댓값을 구해보면

$E[X] = \sum_{i=1}^4p_ix_i = \frac{1}{4}\times2+\frac{1}{4}\times2+\frac{1}{4}\times2+\frac{1}{4}\times2 = 2$
평균 자원량이 2회정도가 된다. 위의 방식보다 0.25회가 줄어들었다.

Shannon의 정보이론을 따르면 위와 같이 각 클래스당 확률이 같을경우 절반을 선택하는 방식이 최선의 방식이라고 한다. Entropy는 위에서 정의한것 처럼 “정보를 표현하는데 필요한 최소 평균 자원량” 이다.
그러므로 이때의 경우 $Entropy = 2$가 된다. (무슨 수를 쓰건 이렇게 구한 값보다 기댓값이 적은 전략은 존재하지 않는다.)

또 다른 경우를 살펴보자. 각각의 카드가 나올 확률이 다를경우

카드 $(s_i)$	a	b	c	d
정답 카드를 뽑을확률 $(p_i = P(s_i))$	$\frac{1}{2}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$
이때 필요한 질문횟수 $(x_i)$	1	3	3	2

1. a 인지 물어본다. <Yes, No>
2. 1번이 < No> 라면 {b, c}중에 있는지 물어본다.
3. 2번이 < Yes> 라면 {b, c}인지 물어보고, < No> 라면 d

위의 기댓값을 구해보면

$E[X] = \sum_{i=1}^4p_ix_i = \frac{1}{2}\times1+\frac{1}{6}\times3+\frac{1}{6}\times3+\frac{1}{6}\times2 = 1.8333...$

이상하게 위와 같은 방식으로 확률을 반으로 나누어 계산했는데 더 낮은 기대값이 나왔다. 여기서 알수 있듯이 확률이 Uniform할때는 최대의 Entropy를 갖고 한곳으로 몰릴때에는 최소의 Entropy값을 갖는다. (=> 극한으로 비교해보면 쉽게 알수 있음)

확률이 몰려있을때는 적은 질문을 필요하고(Entropy가 작다), 확률이 Uniform할때는 많은 질문을 필요하다는 것이다(Entropy가 크다). 정보이론으로 이야기하면, a카드에 물려있을때는 a라고 확신이 크므로 불확실성이 작고, 확률이 Uniform할때는 어느 카드일지 불확실하여 불확실성이 크다. 즉, 정보이론에서 말하는 엔트로피는 “불확실성”이라고 볼 수 있다. 위에서 정의한것 처럼 “불확실성 (uncertainty) 에 대한 척도”인 것이다.

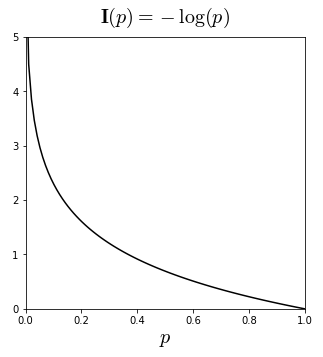
그럼 1.8333…이 최소의 기댓값인지 이론적으로 확인해보자. 확률이 높을때(즉, 1일때) 가장 적은 질문을 필요로하고, 0으로 갈수록 많은 질문을 필요로한다. 이를 수식으로 나타내면 $-Log(x)$와 같아진다.

그래서 각 카드의 질문 횟수는 $I(s_i) = log_2\frac{1}{P(s_i)} = -log_2P(s_i) = -log_2p_i$ 이 된다.

이제 각 카드가 정답일 경우의 질문 횟수를 알아보자. 정답이 a카드일 경우는 다음과 같다. $I(a) = -log_2(\frac{1}{2}) = 1$ 한번만 질문하면 정답을 알수 있게된다. 위에서 구한것과 같다. 정답이 b,c,d일 경우는 다음과 같다. $I(b) = I(c) = I(d) = -log_2(\frac{1}{6}) = 2.5850...$ 2.5850번만 질문하면 정답을 알수있다고 한다. 2.5850번..? 횟수라고 하지만 정수가 아니다. 이렇게 소수가 나온이유는 b,c,d를 정확히 반으로 쪼갤수 없기 때문이다. 현실적으로 이런 최적점에 도달할수 있는 방식은 없지만, 이론상 가장 효율적인 방식이다.



각 카드가 나올수있는 이론상 가장 효율적인 값을 찾아봤다. 어차피 도달하는것은 불가능하겠지만, 로그를 이용해 가장 효율적인 기댓값도 구할 수 있지 않을까?

카드 $(s_i)$	a	b	c	d
정답 카드를 뽑을확률 $(p_i = P(s_i))$	$\frac{1}{2}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$
이론적인 질문 횟수의 최솟값 $(x_i = I(s_i))$	1	$log_2 6$	$log_2 6$	$log_2 6$

$E[X]=\sum_{i=1}^4p_ix_i = \frac{1}{2}\times1 + \frac{1}{6}\times{log_2 6} + \frac{1}{6}\times{log_2 6} + \frac{1}{6}\times{log_2 6} = 1.7925...$

1.7925번이 이론적인 나올 최소값인 것이다. 이론적이기 때문에 도달하지 못할수 있는 값이지만, “무슨 수를 쓰건간에 이렇게 구한 값보다 질문 횟수의 기댓값이 적은 전략은 존재하지 않는다”라는 의미가 내포되어있다.

이렇게 최적의 전략하에서 그 사건을 예측하는 데에 필요한 질문개수에 대한 기댓값을 엔트로피(Entropy)라고 부르며 식은 다음과 같다.

$H=\sum_i^np_iI(s_i) = -\sum_i^np_ilog(p_i)$

엔트로피에 대해 조금 더 알아보면, 각 카드를 알아보기 위해 필요한 질문횟수(정보량)가 달랐다. 정답이 a카드라면 1번의 질문으로 끝이나지만, b/c카드라면 3번의 질문을 거처야 알 수 있었다. 이렇게 a라는 질문의 정보량은 1개의 질문에 해당하지만, b/c의 질문은 3개의 질문이라는 정보량을 가지고 있다. 즉, 질문의 개수가 많으면 그 대상이 지니는 정보량은 많다. => 확률이 작을수록 정보량이 크다. $ I(s_i) = -log_2 p_i $ 식으로 확인해 봐도 확률이 작을수록 정보량이 크다는 걸 알 수 있다.
이와 비슷하게 우리는 보통 매일 보고 듣는 익숙한 것보다는 보고 들은 확률이 낮은 새롭운것에 큰 정보를 얻는다.

이러한 엔트로피를 반영하여 “부호화(Coding)”방식을 사용하는데, 부호화 방식은 데이터의 양을 줄이기 위해 데이터를 코드화하고 압축하는 방식이다. (보통 비트화하여 압축한다.)
비트화하여 정보를 나타내면, a라는 카드는 1개의 비트가 할당되고 b/c는 3개의 비트가 할당 될 것이다. 이렇게 부호화했을 경우, 많이 등장하는 비트에는 적은 비트를 할당하여 전체 부호의 길이가 줄어들게 만든다. 그렇기 때문에 매우 효율적인 코딩이 가능하며, 이러한 원리를 이용한 부호화에는 허프만 부호화(huffman coding) 및 산술 부호화(arithmetic coding) 방식이 있다.