Cross Entropy

May 20, 2022

Cross Entropy : 두 확률 분포사이의 차이를 측정하는 지표

앞서 알아본 Entropy는 불확실성에 대한 척도라고 알아보았다.

예를들면, 완전히 반듯한 동전이 있다고 가정할때, 동전의 앞면과 뒷면이 나올확률은 50:50으로 각각 같다. 이때, 앞면이 나올지 뒷면이 나올지 확실하지 않으므로 불확실성이 높다고한다.
반대로, 동전이 크게 휘어서 앞면과 뒷면이 나올확률이 90:10이라고 하면 앞면이 나올것이라는 확신이 높으므로 불확실성이 낮다.

이렇게 불확실성은 정답을 예측할때 얼마나 확신할수 있는지에 대한 값이다. 이를 섀넌의 엔트로피 수식으로 계산하여 알아보면 다음과 같다.

Shannon’s entropy : 불확실성을 값으로 나타냄

$H=\sum_i^np_iI(s_i) = \sum_i^np_ilog(\frac{1} {p_i}) = -\sum_i^np_ilog(p_i)$

50:50경우

$H=-(0.5log_2(0.5) + 0.5log_2(0.5)) = 1$

90:10경우

$H=-(0.9log_2(0.9) + 0.1log_2(0.1)) = 0.4690$

DL에서는 초기 랜덤변수을 갖는 비교적 높은 불확실성의 모델을 낮을 불확실성을 갖도록 하기위해 KL-Divergece를 이용하여 Optimization 한다. KL-Divergence는 두 확률 분포의 차이를 이용해 얼마나 유사한지 계산하는 방식으로 수식은 아래와 같다.

$D_{KL}(p||q)=E[log(p_i)-log(q_i)]=\sum_{i}p_ilog\frac{p_i}{q_i}=-\sum_{i}p_ilog(q_i)+\sum_{i}p_ilog(p_i)$

( $p: $ 원본확률분포 $q: $ 근사된 분포 $i: $ i번째 item이 가진 정보량 )

DL에서는 방정식을 최소로하여 계산하기 때문에 위에서 KL-Divergence를 다시 정의해보면 아래와 같이 나타낼수 있다.

$D_{KL}(p||q)=-\sum_{i}p_ilog(q_i)+\sum_{i}p_ilog(p_i)=H(p,q) - H(p)$

여기서 $H(p)$는 정답값에 대한 엔트로피인 상수값이므로 DL에서는 무시해도 무관하다.

이렇게 만들어진 $H(p,q)$를 Cross Entropy라고 부르고 수식은 아래와 같으며, DL에서는 이 Cross Entropy를 이용해 잘못된 확률 정보 q에 대한 Entropy값을 최소로하여 p인 원본확률 분포에 가깝게한다.

$H(p,q) = -\sum_{i}p_ilog(q_i)$

즉, Cross Entropy는 정답 확률 분포 p에 대해 q라는 잘못된 확률 정보를 통해서 얻은 엔트로피 값이다. ~~p와 q 모두 식에 있기 때문에 cross entropy라고 이름이 붙혀졌다.~~

가방에 0.8/0.1/0.1의 비율로 빨간/노랑/초록 공이 들어가 있고, 직감에는 0.2/0.2/0.6 비율로 들어가 있을것 같을때, Entropy와 Cross Entropy는 다음과 같이 계산된다. $H(p)=−[0.8log(0.8)+0.1log(0.1)+0.1log(0.1)]=0.63$ $H(p,q)=−[0.8log(0.2)+0.1log(0.2)+0.1log(0.6)]=1.50$
만약에 학습를 통해 서로 p와 q의 확률 분포가 비슷하다면 1.50의 값이 0.63에 가까워 질것이다. 즉, Entropy의 식에 가까워진다. ->

!Tip
MSE VS Cross Entropy

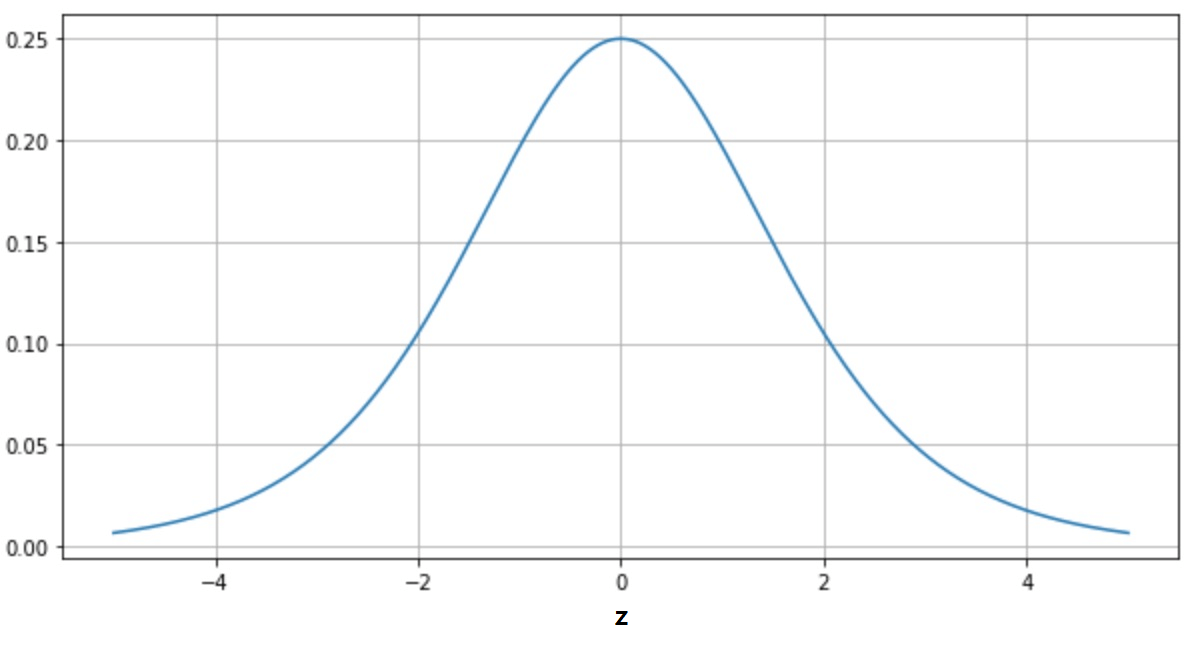
MSE의 경우 Backpropagation 시에 아래와 같이 가중치에 대해서 편미분이 이루어진다. 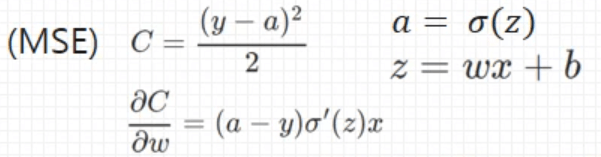이때 편미분값에 Sigmoid 함수의 미분값이 곱해지는데, 이 Sigmoid의 미분 값은 아래와 같이 z가 0일때 최대값을 갖고 0으로 부터 멀어지면 아주 작은 값을 갖는다. 이렇게 아주 작은 값들이 곱해지면서 (a-y)항이 크더라고 결국 아주 작은 값으로 전파되기 때문에 학습속도 저하가 일어난다.