Batch Normalization

Batch Normalization : Batch 단위의 학습데이터를 정규화하여 성능 향상에 도움을 줌

Batch Normalization은 나온지 오래됐지만, 최근 모델에도 빠지지않고 사용되고 있을 정도로 성능향상에 도움이 된다. 먼저 장점들에 대해서 알아보면 아래와 같다.

• 학습 속도 향상
  • Neural Network의 빠른 수렴
• 가중치 초기화(weight initalization)에 대한 민감도 감소
  • Hyper Parameter 세팅의 부담감 감소
• 모델 일반화(Regularization) 효과
  • Overfitting 완화
    
    

학습데이터를 정규화하는 연구는 Normalization, Standardization 등 이전에도 많이 있었다.

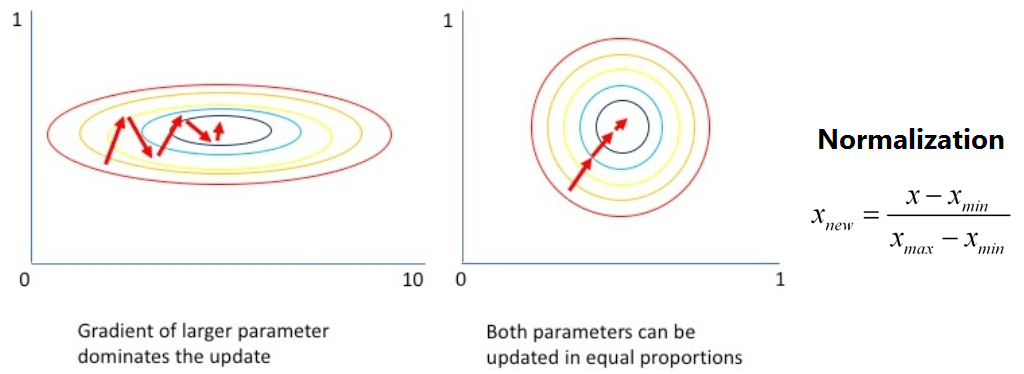
• Normalization : Data 값을 0-1사이로 변환
  
  
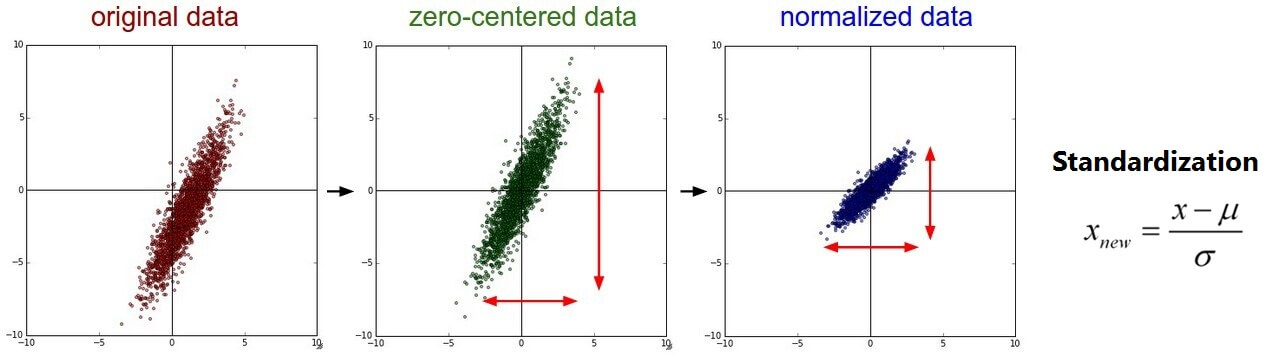
• Standardization : Data 값을 평균 0, 분산 1로 변환
  
  

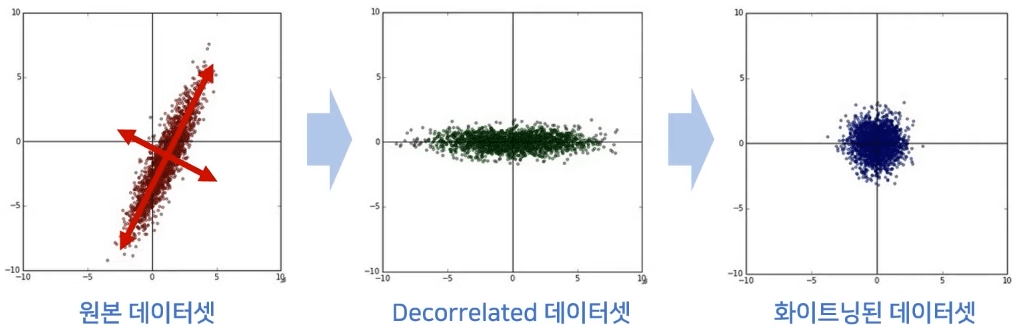
• Whitening: Data 평군이 0이며 공분산이 단위행렬인 정규분포
  -> PCA를 이용하여 새로운 축으로 변환하여 Decorrelated 시킨 후 Standardization 형태로 변환
  
  

하지만 입력데이터를 정규화 하여도 히든 레이어를 거치면서 데이터의 분포는 바뀌게된다. 이것을 Internal Covariate Shift라고 부른다.

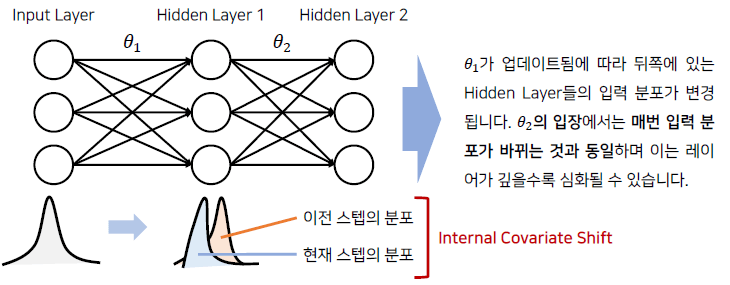
Internal Covariate Shift에서 Covariate Shift는 공변량 변화라고 부르고, 학습시기의 분포와는 다르게 테스트시기에 입력데이터의 분포가 달라지는 현상이다. 예를들어, 어린 아이의 얼굴을 학습 시키고 테스트때는 나이든 얼굴을 Inference한다면 서로의 분포가 달라 예기치 못한 문제가 발생할수있다.

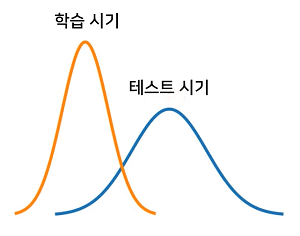
이와 마찬가지로 Training/Test dataset 간의 차이에 대한 문제를 mini-batch간 Input 데이터 관점에서 Covariate Shift가 일어나지 않을까하는 가설을 Internal Covariate Shift라고 한다. Network 내부에도 Whitening이나 Standardization 같은 정규화를 해주면 되지 않을까 싶지만, 단순히 N(0, 1)로 정규화한다면 Sigmoid 및 Tanh의 비선형의 영향력이 감소할수 있다.

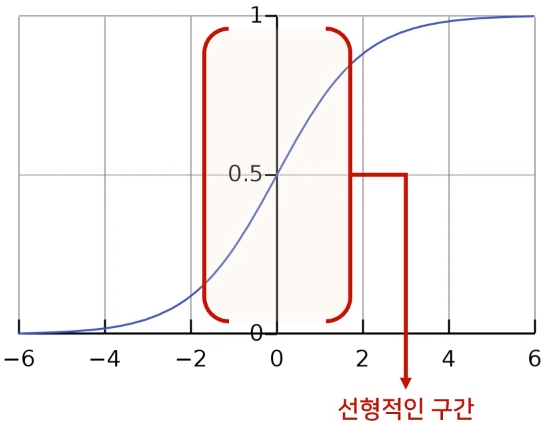
또한, Whitening을 통해 평균이 0으로 가게 되면 Hidden Layer의 Bias영향력이 사라져서 학습이 잘되지 않는다.

이러한 문제 때문에 Batch Normalization에서는 감마($γ$)와 베타($β$)를 사용하여 해결하였다.

mini-batch의 각 Channel들에 대해서 Mean, Variance를 구하고 이를 통해 Normalize를 해준다. 엡실론(ε)을 사용하여 0으로 나누어지지 않게 아주 작은값을 더해준다. 그 후 학습가능한 파라미터(Learnable Parameter) 감마($γ$)와 베타($β$)를 이용하여 Data의 Scale과 Shift를 Backpropagation을 통해 학습해준다. (Batch Normalization은 미분가능!)

위와 같이 Backpropagation시에 파라미터들이 업데이트 되며, Chain Rule을 통해 구할 수 있다.

Test시에는 Test데이터에 대해 Batch Normalization을 진행하는것이 아닌 Train시 구해진 감마($γ$)와 베타($β$)의 평균을 이용하여 구해지게 된다. 이유는 Train 데이터의 Mean값과 Variance값을 사용할 필요가 있으며, Test시에 mini-batch 수가 Train과 같다는 보장이 없기 때문이다. 보통 Train mini-batch들을 이용하여 이동평균(Moving Average)을 구해 Test시에 사용하게 된다.

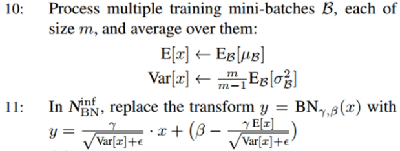
하지만 Internal Covariate Shift 가설이 Batch Normalization이 성능을 높혀주는데에 큰 상관이 없다는 주장이 있다. 배치정규화 직후 랜덤 노이즈를 주어도 성능에 큰 차이가없다는 결과가 나온것이다. 눈으로 봤을때에도 Batch Normalization이 Standard과 비교하여 Normalization이 잘됐다고 보기 어렵다.

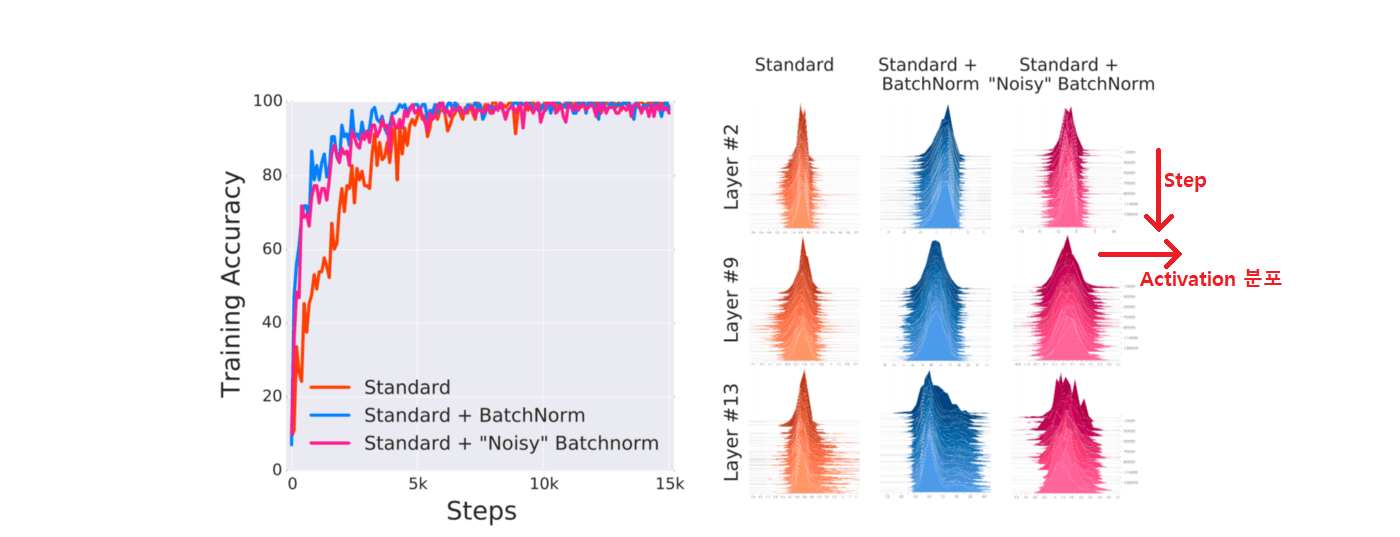
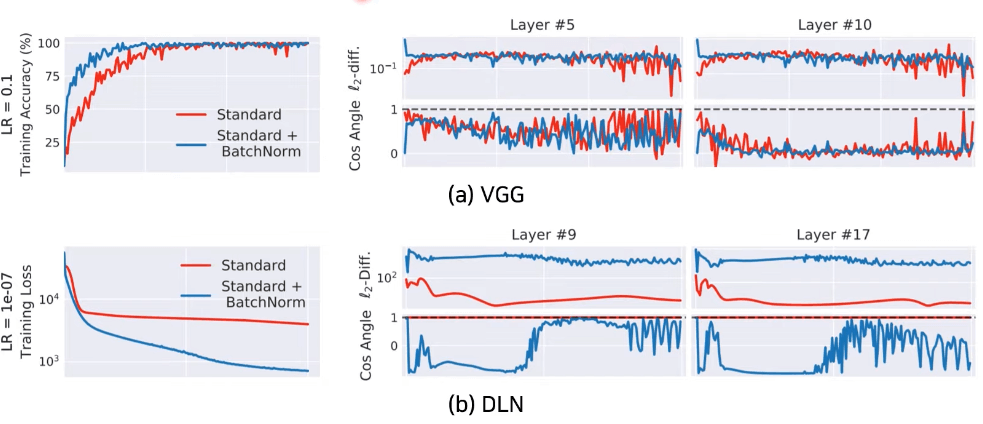
또한, 아래의 그림과 같이 동일 이미지에 대해 특정 Layer에서 Weight Update전 기울기와 Update후 기울기를 L2-diff 및 Cos Angle 그래프로 보면, Batch Normalization을 사용해도 Internal Covariate Shift(ICS)가 그대로이거나 오히려 증가하는것을 볼수 있다. (기울기 차이가 크면 ICS가 크고 / 작으면 ICS가 작다)

그렇다면 Batch Normalization이 잘 동작하는 이유는 무엇인지 살펴보면, 아래의 그림은 Weight Domain에 대한 Loss Landscape를 나타낸 그림이다. 왼쪽은 들쭉날쭉한 Loss 기울기를 갖는 반면 오른쪽은 완만한 기울기를 갖는다. 즉, Batch Normalization는 Optimization Landscape를 부드럽게 만들어, 큰 LR을 사용해도 초기 기울기 방향과 유사할 가능성이 높다. 즉, 아래와같이 Gradient가 안정적으로 감소할수 있게 도와주며, 학습도 빠르게 진행될수 있도록 도와준다.(Batch Normalization, Residual Connection 등이 Smoothing을 이끌어낸다고 알려짐)

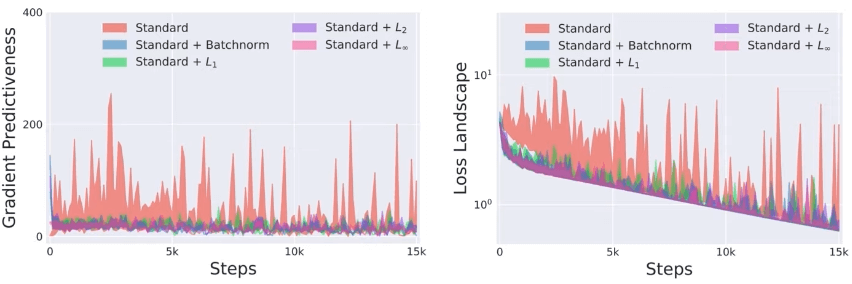
아래의 그림이 위 내용을 그래프로 보여주고있다. 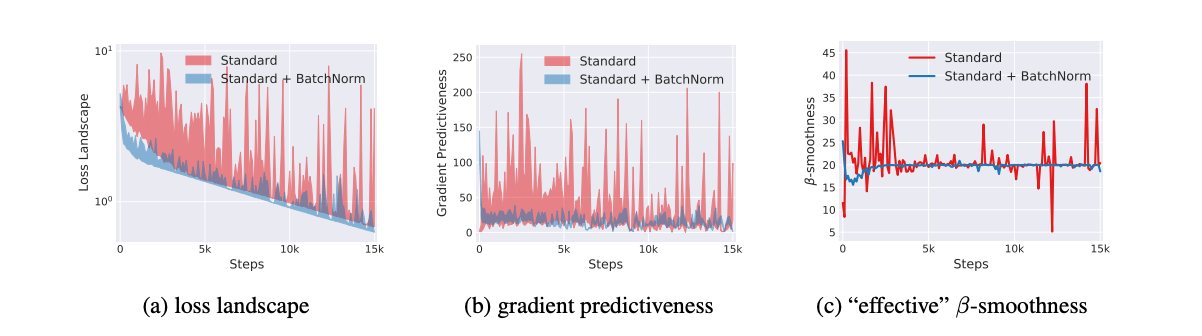첫번째 그림은 Loss에 따른 기울기를 보여주고있다. Batch Normalization의 Loss가 더 안정적으로 떨어지는것을 볼수있다.

두번째 그림은 기울기 예측성(Predictiveness)을 보여주고 있다. 초기 가중치의 위치에서 기존의 기울기 방향과 다 양한 Step에서의 기울기 방향의 차이를 보여주는것이다. 그러므로 기울기가 많이 요동친다고 하면 학습의 신뢰도가 떨어지는것이고, 안정될수록 신뢰도가 높다고 판단할수 있으며, Batch Normalization의 그래프가 더 안정적인것을 볼수있다. 예를들어 특정 위치의 기울기에 대해서 Learning Rate를 크게크게 움직여도 기울기의 변화가 거의 없으므로 Batch Normalization이 Learning Rate에 둔감하다는것을 확인할수 있다.

세번째 그림은 “effective” β-smoothness를 보여주고 있는데 β-smoothness는 Lipschitz함수를 통해 확인할수 있다. Lipschitz-Continuous Function은 “연속적이고 미분이 가능하고 어떠한 두 점 사이의 거리를 일정 비 이상으로 증가시키지 않는 함수”를 의미한다.

$\frac{\left|f(x_1)-f(x_2) \right|}{\left| x_1-x_2\right|}\leq K$

그림에서 보는것과 같이 큰 Step만큼 이동한 뒤에도 안정적인 그래프를 보이고있다.(Lipschitzness가 향상된다)
그러므로, 큰 Step만큼 이동한 뒤에도 기울기의 방향이 초기와 유사할 가능성이 높으므로, 파라미터에 대한 Loss Function이 Lipschitz-Continuous라면 상대적으로 안정적이게 학습할 수 있는 것이다. (Neural Network가 안정적임을 증명할때 많이 사용되곤 함)

Batch Normalization이 아니더라고 Smoothing 효과가 있는 기법을 사용하면 성능이 향상 된다는 글도 있다. 이는 Internal Covariate Shift를 증가 시킴에도 성능을 증가 시킬수 있다는 것을 보여주고있다.