Eigen-value, Eigen-vector, Eigen-decomposition

Eigen-vector : 선형변환 후 방향이 변하지 않는 벡터
Eigen-value : Eigen-vector의 길이 변화의 수치값
Eigen-decomposition : 특정 행렬을 Eigen-vector와 Eigen-value로 분해하여 성질을 파악

Eigen-vector, Eigen-value

행렬은 공간의 선형변환을 일으킨다. 예를들어 회전 변환 / 투영 변환 등의 변환은 행렬에 의한 공간의 변형이 일어나 생긴 결과물이다.
위에서 Eigen-vector와 Eigen-value는 선형변환 후 방향이 변하지 않고 길이만 변하는 수치라고 하였다. 즉, 어떠한 벡터 $x$에 선형변환 A을 취했을때, 벡터 $x$의 방향은 변하지 않고 길이만 변하는 수치를 Eigen-vector와 Eigen-value라고 한다.

정의 : 임의의 $n × n$행렬 A에 대하여, 아래의 수식을 만족하는 nontrivial solution(영행렬이 아닌 해가 존재) 벡터 $x$가 존재한다면 $λ$는 행렬 A의 고윳값이라고 할 수 있다.
$Ax = λx$ ($x$: Eigen-vector / $λ$: Eigen-value)

위 수식을 성립하기 위한 조건은 첫번째, 벡터 $x$가 0이여야한다. 두번째, $(A - λI)$가 0이여야한다. 첫번째의 경우 벡터$x$=0, 무한한 $λ$의 값을 갖게 될것이다. 그러므로 두번째 조건을 만족하기위해서는 $(A - λI)$가 역행렬을 갖으면 안된다. nontrivial solution 벡터 $x$를 구하기 위해서는 $(A - λI)$가 역행렬을 갖으면 안되므로 아래와 같이 특성방정식 (characteristic equation)을 만족해야 된다.

$Ax = λx$ =>$(A - λI)x = 0$ =>$det(A - λI) = 0$

예를들어, $ A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} $의 행렬이 있을때,

$det(A - λI) = 0$

을 전개하면,

$det(A - λI) = det\begin{pmatrix}\begin{bmatrix} 2-λ & 1 \\\\ 1 & 2-λ \end{bmatrix}\end{pmatrix} = 0$
$=> (2-λ)^2-1 = λ^2-4λ+3 = 0$

그러므로 $λ_1 = 1, λ_2 = 3$ 이다. 즉, 행렬 $A$의 고윳값은 1, 3이다.

이에 맞는 Eigen-vector를 구해보면, 아래와 같은 연립방정식이 성립되야 된다.

$Ax = λ_1x$
$ => \begin{bmatrix} 2 & 1 \\\\ 1 & 2 \end{bmatrix} \begin{bmatrix} x_1 \\\\ x_2 \end{bmatrix} = 1\begin{bmatrix} x_1 \\\\ x_2 \end{bmatrix}$
$ => \begin{bmatrix} 2x_1+x_2 = x_1 \\\\ x_1+2x_2 = x_2 \end{bmatrix}$
$ => \begin{bmatrix} x_1 \\\\ x_2 \end{bmatrix} = \begin{bmatrix} 1 \\\\ -1 \end{bmatrix}$

따라서,
$λ_1 = 1$일 때의 Eigen-vector는 $\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 1 \\ -1 \end{bmatrix}$와 같고,
$λ_2 = 3$일 때의 Eigen-vector는 위와 같이 계산했을때, $\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$와 같다.

두번째 결과값을 토대로 그래프로 그려 쉽게 알아보면, $x = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$에 대하여, 행렬 $A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}$의 선형 변환을 시켜보면 아래와 같은 그래프가 나타나게 된다. 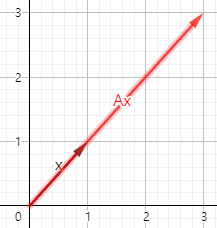이는 $x$가 방향은 변하지 않고 크기만 3배가 되었고, $Ax = λx$ 식을 만족하는 결과가 되었다.

즉, 행렬 $A$에 대해서 Eigen-value $λ_2 = 3$일 때의, Eigen-vector $x = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$이고,
Eigen-value $λ_1 = 1$일 때의, Eigen-vector $x = \begin{bmatrix} 1 \\ -1 \end{bmatrix}$이다.

Eigen-decomposition

Eigen-decomposition은 Eigen-vector와 Eigen-value로 분해하여 성질을 파악하며, 행렬 거듭제곱의 계산이 수월해진다.

예를들면, $A = PDP^{-1}$형태의 수식을 많이 보았을 것이다. 이때 $D$는 대각행렬이다.
위식을 이용하여 $A^2 = (PDP^{-1})(PDP^{-1})=PD^2P$ 와 같이 계속 진행하여 결국 $A^k = PD^kP^{-1}, (k≥1)$이라는 일반화 수식을 이끌어 낼 수 있게된다. 이때, 대각행렬 $D$는 행렬의 대각선의 원소만 존재하기 때문에 쉽에 거듭제곱을 할 수 있어, 효율적으로 계산을 진행할 수 있게된다.

만약 Eigen-decomposition를 구하고 싶다면, 가역행렬 $P$는 행렬 $A$의 Eigen-vector들이며 Linearly Independent 해야한다. 즉, 같은 성분을 갖은 벡터 $a_i∈\mathbb{R}^{n×1} \ for \ i=1,2,…,n$이 있을때, $c_1a_1+c_2a_2+…+c_na_n=0$을 만족하는 상수 $c_1,c_2,…,c_n$이 모두 0이여야 한다. 이때 벡터 $a_1, a_2,..,a_n$은 Linearly Independent라 한다.
예를들어, $R^2$의 두벡터 $a_1=\begin{bmatrix} 1 \\ 0 \end{bmatrix}, a_2=\begin{bmatrix} 0 \\ 1 \end{bmatrix}$는 $c_1a_1 + c_2a_2$의 해가 유일하게 $c_1, c_2 = 0$ 밖에 없기 때문에 선형 독립이다.

조금 더 자세히 알아보면, 임의의 $n × n$행렬 $A∈\mathbb{R}^{n×n}$에 대해 $n$개의 Eigen-value와 Eigen-vector를 얻을 수 있고, $Av_i = λ_iv_i \ (for \ i = 1,2,…,n)$에서 Eigen-vector를 열벡터로 갖는 고유벡터행렬 $V∈\mathbb{R}^{n×n}$와 Eigen-value를 대각성분으로 갖는 고윳값행렬 $\Lambda∈\mathbb{R}^{n×n}$로 나타내면, 아래와 같이 나타내어 진다.

$AV = {\Lambda}V = \begin{bmatrix} λ_1v_1 & λ_2v_2 & ... & λ_nv_n \end{bmatrix}$

다시 수식을 정리해보면,

$ V = \begin{bmatrix} v_1 & v_2 & ... & v_n \end{bmatrix} \ \Lambda = \begin{bmatrix} λ_1 & 0 & ... & 0 \\\\ 0 & λ_1 & ... & 0 \\\\ ... & ... & ... & ... \\\\ 0 & 0 & ... & λ_N \end{bmatrix}$
=>$AV = \begin{bmatrix} λ_1v_1 & λ_2v_2 & ... & λ_nv_n \end{bmatrix} = \begin{bmatrix} v_1 & v_2 & ... & v_n \end{bmatrix} \ \begin{bmatrix} λ_1 & 0 & ... & 0 \\\\ 0 & λ_1 & ... & 0 \\\\ ... & ... & ... & ... \\\\ 0 & 0 & ... & λ_N \end{bmatrix} = V{\Lambda}$

이때 $V$가 가역행렬이므로 아래와 같이 정리가 가능하다.

$AV = V{\Lambda}$
$∴ \ A = V{\Lambda}V^{-1}$

만약 행렬 $A$가 대칭행렬이라면 Eigen-value가 실수이고 Eigen-vector가 서로 직교(orthogonal)하는 약간 특이한 성질이 있다. 대칭행렬의 성질은 아래와같다.

$A = A^T$

행렬 $A$를 Eigen-decomposition할 수 있다면, 아래의 수식이 성립한다.

$A = V{\Lambda}V^{-1} = A^T = (V{\Lambda}V^{-1})^T = (V^{-1})^T{\Lambda}^TV^T$

${\Lambda}$는 대각행렬이므로 아래와 같이 나타낼수 있다.

${\Lambda} = {\Lambda}^T$ $(V^{-1})^T = (V^T)^{-1}$

이를 바탕으로 위 수식을 다시 정리하면,

$V{\Lambda}V^{-1} = (V^T)^{-1}{\Lambda}V^T $ $V^T = V^{-1}$ $VV^T = V^TV = I$

즉, 실수인 대칭행렬은 Eigen-decomposition가 가능하며, 대칭행렬 $A$의 고유벡터행렬 $V$는 직교행렬이다.